II - Energy #
Energy Is in the Air; You Can’t See It, but It’s There. #

Wind turbines on a wind farm in Western Australia. Image courtesy of Getty Images.
Introductory Thoughts #
A fluid in motion has remarkable abilities, as indicated by the constructive power generated by wind turbines, all the way to the destructive power unleashed by hurricanes. This capability comes from a fluids ability to attain and deploy vast amounts of energy.
Total Pressure #
A fluid can attain energy through two mechanisms; static pressure, and dynamic pressure. Dynamic pressure is the energy associated with the momentum of a fluid. Static pressure describes the energy available for a fluid to push adjacent units of fluid. Static pressure doesn’t have direction, it pushes equally on all sides.
Energy can’t be created or destroyed (First Law of Thermodynamics), so energy lost from static pressure is gained in its dynamic pressure. This behavior is described by Bernoulli’s Principle. A fluid can have both types of energy at the same time. The sum of these two energy types is termed Total Pressure.
\[Total Pressure = Static Pressure + Dynamic Pressure\]Static and dynamic pressure are like yin and yang.
A fluid in motion has dynamic pressure. In the abscense of any objects within the path of the flow, the energy is most in the form of dynamic pressure. However, if 100% of the energy is dynamic pressure, it flows in straight lines because it doesn’t have any ability to change its flow direction.
When an object appears in the path of the flow, To guide itself around, the flow near the blade is forced to exchange some of its dynamic pressure into static pressure. The push the static pressure field provides to the flow is what allows the flow to move around the object. However, the resulting static pressure field also generates a force which pushes on the object.
The static & dynamic pressure vary in relation to streamline curvature. As a useful rule of thumb, a concave inflection of the streamline results in higher static pressure and lower dynamic pressure, and a convex inflection results in lower static pressure and higher dynamic pressure. For the curious, the mathematics as to why this occurs can be found here.
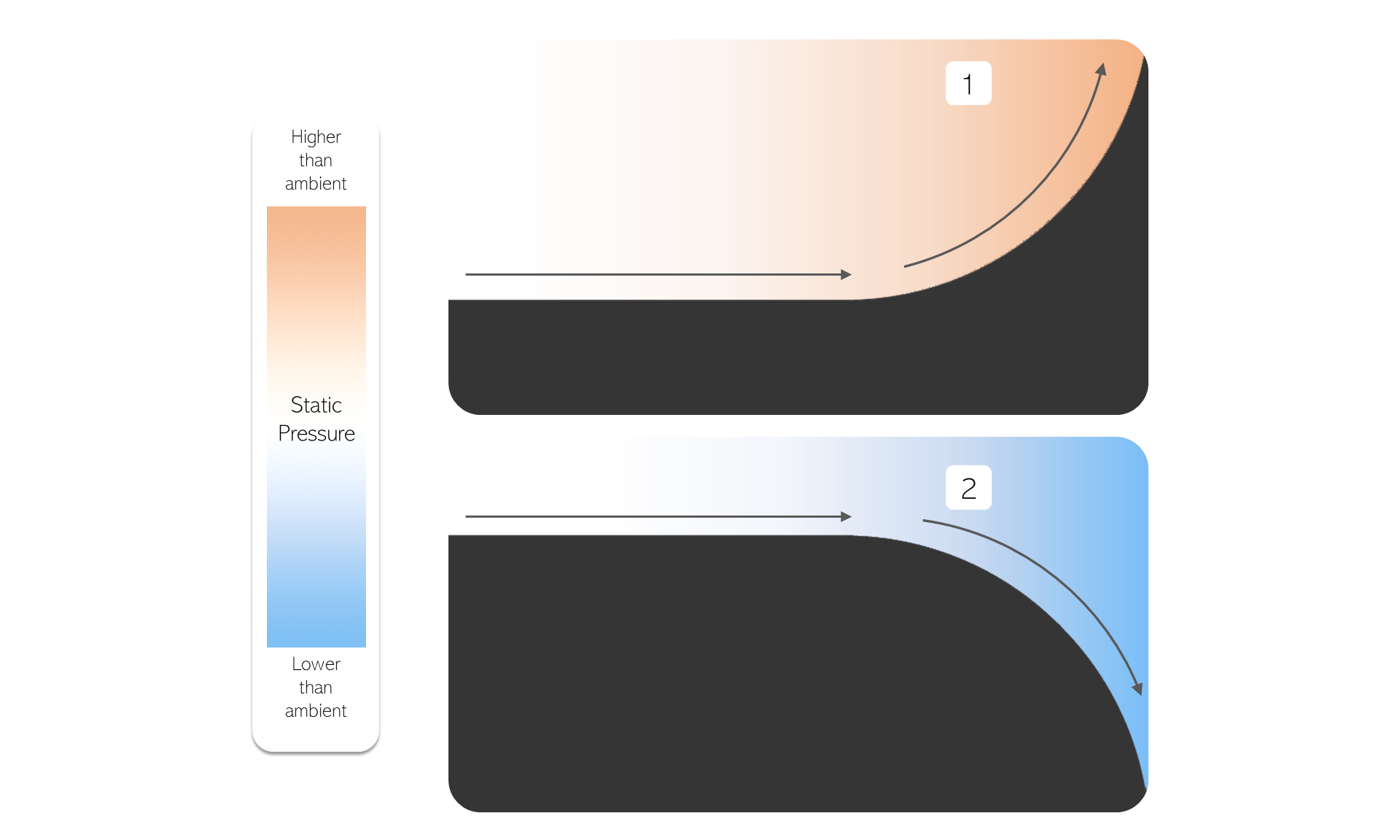
| Point | Behavior |
|---|---|
| 1. | A concave inflection of the streamline results in higher static pressure. |
| 2. | A convex inflection of the streamline results in lower static pressure. |
The static pressure field explains why air flows around things, and not at them (as discussed in first article, I - Form). The static pressure field projects the influence of the body beyond its perimeter, giving the flow ‘advance warning’ that something is coming. This static pressure field pushes the flow into the path of least resistance around the body, from areas of high to low static pressure.
Displaying the static pressure field around the streamlined body provides new insight.
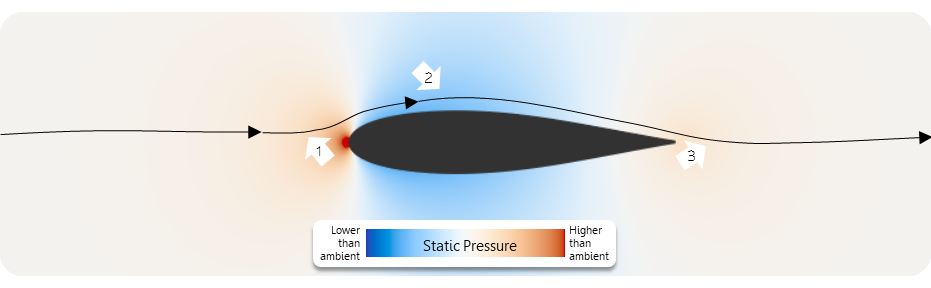
| Point | Behavior |
|---|---|
| 1. | The high static pressure ahead of the body starts to push the flow aside early, creating divergence. |
| 2. | The lower static pressure on the sides acts to pull the flow next to the surface, creating convergence. |
| 3. | Finally, the higher static pressure at the back of the body realigns the flow at the trailing edge. |
Aerodynamicists only use ‘pull’ in the colloquial sense, as technically static pressure can only push. For example, a vacuum doesn’t pull particles inside it by creating ‘negative pressure’. Instead, a vacuum lowers its inside static pressure slightly below ambient (it’s still positive), and the higher static pressure on the outside pushes the particles inside.
Shown below is a cross section of an airplane wing with both the static and dynamic pressure fields. Because of Bernoulli’s Principle, they are virtually the inverse of one another.
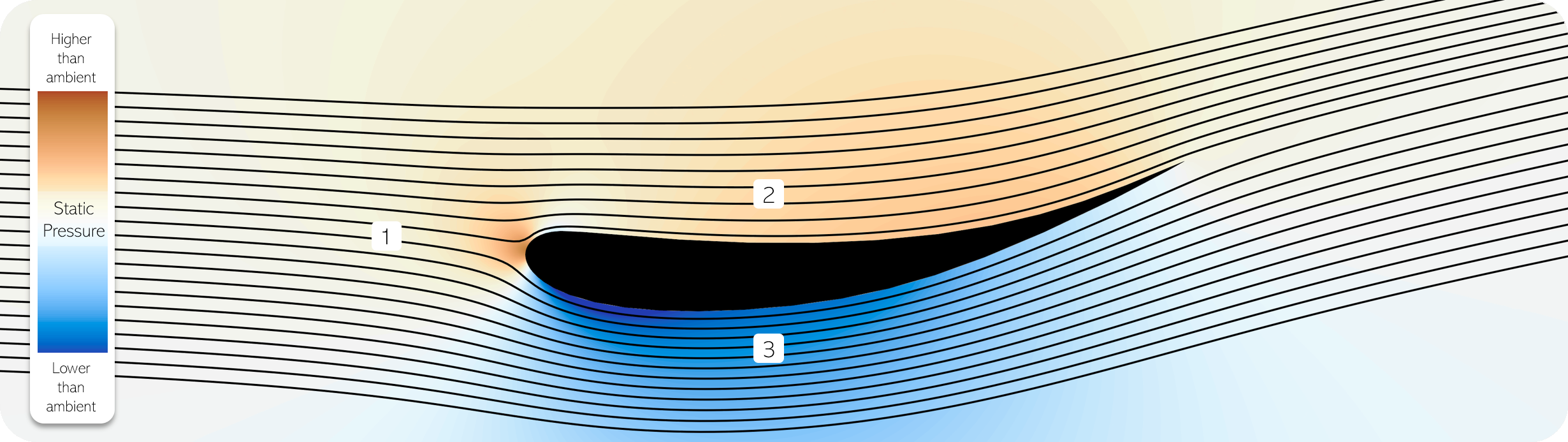
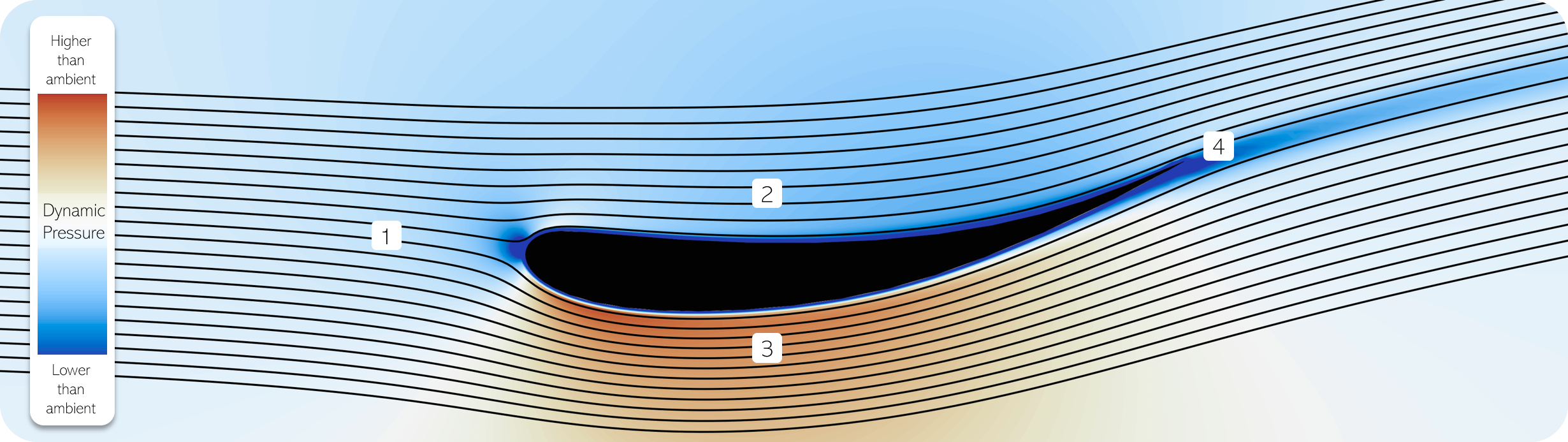
| Point | Behavior |
|---|---|
| 1. | The streamlines approach the blade head on. |
| 2. | High static pressure (and low dynamic pressure) on the upper surface push the flow aside. |
| 3. | Low static pressure (and high dynamic pressure) on the lower surface pull the flow to the same side. |
| 4. | The near wall region doesn’t seem to abide by Bernoulli. This is explored in the next article. |
Real World Applications #
These concepts are best understood by considering a wind turbine. Wind turbines extract energy from the air and convert it into electrical energy.

Wind turbines are placed in areas of high wind speeds, as high wind speeds have high dynamic pressure. Dynamic pressure is the energy associated with the momentum of a fluid.
PICTURE
The wind pushes on the individual blades of the turbine, rotating them and creating electricity. The push comes from the dynamic pressure turning partially into static pressure. Static pressure describes the energy available for a fluid to push adjacent units of fluid. Static pressure doesn’t have direction, it pushes equally on all sides. The push the static pressure field provides to the flow is what allows the flow to move around the turbine blade. However, the resulting static pressure field also generates a force which pushes on each fan blade, rotating the assembly and creating electricity.
PICTURE
Once the air flows past the blade, the static pressure goes back into dynamic pressure.
However, by virtue of the flow expending energy on the turbine blades, the flow downstream of the turbine has a diminished energy level, and therefore has less energy to spin other turbines. This is why the layout of a wind farm is so important. If subsequent turbines are directly downstream of the first, the flow has a significantly diminished ability to spin blades and create energy.
This effect can be seen below.

The layout of these turbines has been optimized for the most likely flow direction, which minimizes influence of upstream turbines on the downstream ones. However, wind direction is variable, and the photographer captured an instance of the wind direction being unfavorable for the layout. Image courtesy of phys.org.
–>
In a similar vein, the bodywork of an airplane or a car is designed to force the flow to create static pressure which acts on the bodywork to generate useful forces.
So it’s been established that a fluid in motion has energy via total pressure. However, most real-world scenarios involve an object moving through a stationary fluid, so how is this relevant to aerodynamics?
To help answer that, consider the image below. Is it at all possible to tell whether the particles are moving past the camera, or if it’s the camera that’s moving quickly through the particles?

It’s not, and the same idea applies in aerodynamics. From the point of view of the object, the fluid is moving. From the point of view of the fluid, the object is moving. The behavior to an outside observer is identical in every way, so which frame is considered comes down to preference.
In wind tunnel testing & in simulation, it’s much easier to keep the object stationary and have fluid move past it. As a result, the standard is to think of the fluid in motion, as it’s less mental overhead than having to constantly switch between the two frames of motion. Henceforth, unless otherwise stated, it is be assumed the object is stationary and the fluid is moving.
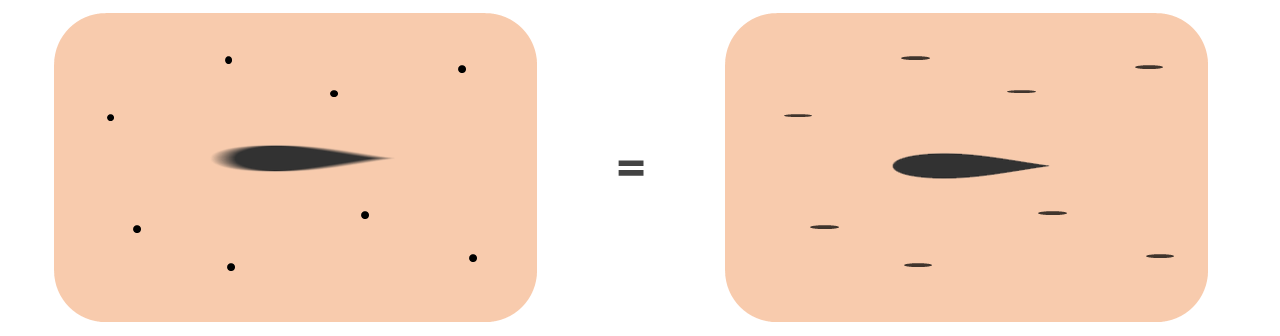
Concluding Thoughts #
In review, recognizing where the energy is and what state it’s in is important for successfully deploying it to do useful work. A wind turbine requires forcing the flow to exchange its dynamic pressure into static pressure, static pressure which generates a force on the turbine blade allowing it to spin.
Unfortunately, using the energy in this way carries some consequences. This is explored in Part III, where the reader is introduced to friction and how it saps energy from the flow.
For questions or clarifications on this, or any other article, reach out to Nav@WorksAero.com.